こんにちは。大田です。
最近、 キーボードを新調してタイピングの音が小さくなりました。
タイプミスも減ってもしかして?なめらかな?タイピングに?なってる?って実感してます。
以前のキーボードは合ってなかったのかも。しれない。
つい先日、OpenAIからSoraが発表されましたね。
すごい。ピクサー感あるのもある。

昔、AfterEffectとかMotionとか使って四苦八苦しながらCM作ってたことがあるんですけど、これからどうなるのかなぁと想いを馳せています。
ブワーっとアニメーションしたりする時はレンダリングに時間がかかるから、その間とりあえず一服するかを繰り返してたのに、これからはとりあえす世界観をテキストで打ち込んで、仕上がるまで一服するかみたいになるんでしょうか。
動画生成も1年前に比べるとものすごく進化してて、ドッグイヤーって呼ばれてたけどこれって何イヤーなんだろう。
GoogleがGeminiを発表したし、OpenAIはチームプランをつい先日にも発表してたし、情報収集が追いつきません。
そういえば情報って科目も増えてますねって話したのも思い出し、
昨今ロジカルシンキング、とか論理的思考とかよく聞く言葉ですけど、そもそも論理って何?というのが発端でニュートンの「ニュートン別冊 楽しみながら身につく論理的思考」本を読んだのを思い出しました。
https://www.newtonpress.co.jp/separate/back_general/mook_220105-3.html
前置きが長くなりましたが、今回は論理とプログラミングです。
本書の内容を紹介しつつ、プログラミングではどういうことかも考察しつつ記事にしたためたいと思います。
論理的であるということ
本書では、論理的に考えるということは、基本的には「思考の道筋を整理して明らかにする」そして、思い込みを排除してさまざまな問題を考えていくのが論理的思考と述べられてます。
そのような思考の基礎になってるのが、論理学という学問で4つの原理があり、
・同一の原理
・矛盾の原理
・排中の原理
・充足理由の原理
がその原理だそうです。
同一の原理
AはAである、と表すもの。哲学者・数学者のゴットフリート・ヴィルヘルム・ライプニッツが考えた。
# このコードは、変数aが自分自身と等しいことを確認しています。結果はtrueです、つまりaはaと同一です。
let a = 5;
console.log(a = a); // true矛盾の原理
Aは非Aでない、と表すもの。アリストテレスが考えた。
# このコードでは、bが5より大きい、かつ、5以下であるという二つの条件を同時に満たすことは不可能であることを示しています。そのため、結果は常にfalseです。
let b = 10;
console.log(b > 5 && b <= 5); // false排中の原理
Aかまたは非Aである、と表すもの。
この球は赤い、この球は白い、の間にはこの球は桃色、というのもありうる。
# このコードは、cが20以上であるか、20未満であるかのどちらか一方が必ず真であることを示しています。これは排中の原理を表しています。
let c = 20;
console.log(c >= 20 || c < 20); // true充足理由の原理
なぜそうなるかという十分な理由がなければ真実でない。とライプニッツは考えた。
十分な理由を根拠とよび、根拠をもとに主張することを帰結という。
もし天気ならば遊びに出かける。等。
let number = 10;
let isEven = (number % 2 = 0); // この行が「十分な理由」2で割り切れるかどうか
console.log(isEven); // true
プログラミングの基礎ですね。基礎と言うか、その原理で組み立てると言うか。処理をするというか。
この原理が定義されていないと書けないと言うか、その原理を定義することを仕様を定義すると言うか。
なんとなく伝わりましたでしょうか。
この原理の定義がおかしかったりするとバグったりします。😇
(それ以外にもいろんな事象でありますが…)
命題
事実か事実でないかを判断できる文が命題と言われてます。
プログラミングでは真偽値という言葉をよく使います。TrueまたはFalse。
アイザック・ニュートンはイギリス人である → 事実 のためこれは真の命題
りんごはユリ科である → バラ科なので事実でない ためこれは偽の命題
りんごはあかいですか? → 疑問文なので命題ではない
賛成か反対を選びなさい → 命令文なので命題ではない
なんて綺麗な花なんだろう → 感想文なので命題ではない
論理的思考は、観察できる事実、または根拠のある事実だそうです。
事実を正確に定義できるのかという哲学的問題は別にあるそうです。
そして、命題が論理学の最も基本的な概念である。との事です。
リンダ問題
リンダという女性がいる。彼女は31歳で独身。非常に聡明ではっきりものを言う性格だ。
彼女は学生時代に哲学を選考していた。人種社別や社会正義の問題に強い興味を持ち反核運動にも参加していた。
下に示した2つの選択肢のうち、リンダはどちらに当てはまる可能性が高いだろうか。
A:リンダは銀行の窓口係である。
B:リンダはフェミニズム運動に熱心な銀行の窓口係である。
はい。みなさんはどちらが正解かと思いますか?
正解は?
オッカムのかみそり
12世紀ころから、アリストテレスの「世界にはじまりはない」という哲学と、キリスト教の「世界は神によって想像された」という考えが激しく衝突していたようです。
そこで神学者のトマス・アクィナスは神学が最上位の学問で、その下に哲学を唱えました。
これに対してオッカムが神学と哲学を分離することを唱えました。
オッカムは「明確に知覚できない(または十分な根拠をもたない)存在や概念を認めるべきではない」、「必要以上の仮定はするべきではない」と主張しました。
これをオッカムのかみそりと呼んだそうです。
いまそれ考えなくて良くない?とか思う時は、オッカムのかみそりで切っていい?っていうことなんですね。
三段論法
三段論法は、論理学における推論の形式の一つで、二つの前提から一つの結論を導き出す方法です。この形式は、古代ギリシャの哲学者アリストテレスによって体系化されました。
大前提:すべての人間は死ぬ。(全称肯定)
小前提:ソクラテスは人間である。(特称肯定)
結論:ソクラテスは死ぬ。
三段論法は、その形式が正しく前提が真であれば、結論もまた真であると保証される推論の形式です。
本書では誤った三段論法の例が紹介されてまして、
正しい推論と誤った推論を三段論法の形で表すと、
正)
前提1:てるてる坊主理論は正しいならば今日は晴れる(AならばB)
前提2:今日は晴れなかった(Bでない)
結論:てるてる坊主理論は正しくない(Aでない)
誤)
前提1:てるてる坊主理論は正しいならば今日は晴れる(AならばB)
前提2:今日は晴れた(Bである)
結論:てるてる坊主理論は正しい(Aである)
なにが間違った使い方かわかりますか?
正解は、AならばBという前提で、Bでないに続き、ゆえにAでないに続いています
誤った方は、AならばBという前提で、Bである、ゆえにAであるが論理の飛躍だそうです。
論理の飛躍、わかりますか?
GPT先生にもう少し聞いてみましょう。
論理の飛躍とは、議論の中で前提から結論への推論が不十分であるか、あるいは全くサポートされていない場合に発生します。これは、議論の中で必要な論理的なステップが欠けているか、あるいは無視されている状態を指します。その結果、結論が前提から論理的に導かれていないため、聞き手や読み手にとって結論が突然または無根拠に感じられることがあります。
論理の飛躍の例
例1:不十分な証拠に基づく結論
前提:私の友人の一人が海で泳ぎながらサメに遭遇した。
結論:だから、海で泳ぐのは危険だ。
この例では、一人の友人の経験から海で泳ぐ全般に関する広範な結論を導いています。しかし、この一件だけで海で泳ぐ全ての状況が危険であると結論づけるのは論理の飛躍です。多くの人が安全に海で泳いでいる事実が無視されています。
例2:関連性のない前提からの結論
前提:今日は雨が降っている。
結論:だから、私は試験に落ちるだろう。
この例では、天気と試験の結果という全く関連性のない二つの事柄を結びつけています。雨が降っていることが試験の結果にどのように影響するのか、論理的なつながりが示されていません。これも論理の飛躍の一例です。
論理の飛躍を避けるために
論理の飛躍を避け、より説得力のある議論を構築するためには、以下の点に注意すると良いでしょう。
段階的な推論:前提から結論へと自然に導かれるよう、論理的なステップを明確にする。
証拠の提供:結論を支持するために、関連する証拠やデータを提供する。
仮定の検証:議論の中で暗黙のうちに行われている仮定を明らかにし、それらが妥当であることを確認する。
論理の飛躍は、議論の信頼性を損ない、聞き手や読み手を納得させる能力を弱めるため、注意深く避ける必要があります。はい。なんか話しがぶっ飛んでたら、それは論理が飛躍してると言うことですね?
正しい三段論法と誤った三段論法の例
前提が正しければ結論も必ず正しい
| 前提1 | 前提2 | 結論 | |
|---|---|---|---|
| AならばB | A | ゆえに | B |
| AならばB | Bでない | ゆえに | Aでない |
| AならばB | BでないならばC | ゆえに | AならばC |
| AまたはB | Aでない | ゆえに | B |
間違いは前提が正しくても結論が正しいとは限らない
| 前提1 | 前提2 | 結論 | |
|---|---|---|---|
| AならばB | B | ゆえに | A |
| AならばB | Aでない | ゆえに | Bでない |
| AならばB | AならばC | ゆえに | BならばC |
| AまたはB | A | ゆえに | Bでない |
いくつかの推論から結論を導くことを推論というそうです。
他にも推論があるよ
帰納法
個別の事例をあげて、全体の性質などより普遍的な結論を導く推論のこと。
例えば、海外で何度も危険な目にあった人が外国は怖いと結論づけてしまう。など。
実は帰納法はすべて論理的にはあやまった推論なんだそうな。😲
演繹法(えんえきほう)
帰納法とは逆に、普遍的なことを述べた前提から個別のことについて述べた結論を導く推論。
例えば、すべてのきのこは菌類である、エノキタケはキノコである、ゆえにエノキタケは菌類である。
こっちは論理的に正しい推論なんだそう。
なんとなーくプログラミングでいえばオブジェクト指向プログラミングにおけるクラスの定義に似ているかもしれません。
class Car {
constructor(brand, model, year) {
this.brand = brand; // 車のブランド
this.model = model; // 車のモデル
this.year = year; // 製造年
}
// 車の情報を表示するメソッド
displayInfo() {
console.log(`This is a ${this.year} ${this.brand} ${this.model}.`);
}
// 車の年式を更新するメソッド
updateYear(newYear) {
this.year = newYear;
console.log(`The car's model year has been updated to ${this.year}.`);
}
}
// Carクラスのインスタンスを作成
const myCar = new Car('Toyota', 'Corolla', 2020);
// 車の情報を表示
myCar.displayInfo(); // This is a 2020 Toyota Corolla.パラドックス
論理的に問題なさそうと思っていても、より深く考察することで矛盾を含んでいることだそうです。
例えば、全能のパラドックスというものがあり、全能者は自分でも持ち上げられない程の重い石を作ることができるのか?です。
もし作れたら全能者は全能ではなくなり、作れないとしても全能者ではなくなるという矛盾です。
他にもアキレスと亀という有名な話もあり、これは亀も前進するのでアキレスが亀に追いつくことはできないという説です。
他にも砂山から砂を1粒取ったとしてもそれは砂山である。
これを定義したとして、ずっと繰り返すと砂粒しか残らないけどこれも砂山だっけ…。という曖昧な真偽の解決にファジー論理があるそうです。
数字で表すと…?
面白い例文がありましたので紹介します。
社長が会社のイベントで誕生日が来た人にはその人に特注のグラスをプレゼントしよう。休みの日が誕生日だった場合は休みがあけた日に渡すことにしよう。
そこで社員が、同じ誕生日の人がいたら人数分用意されるんですか?といった。
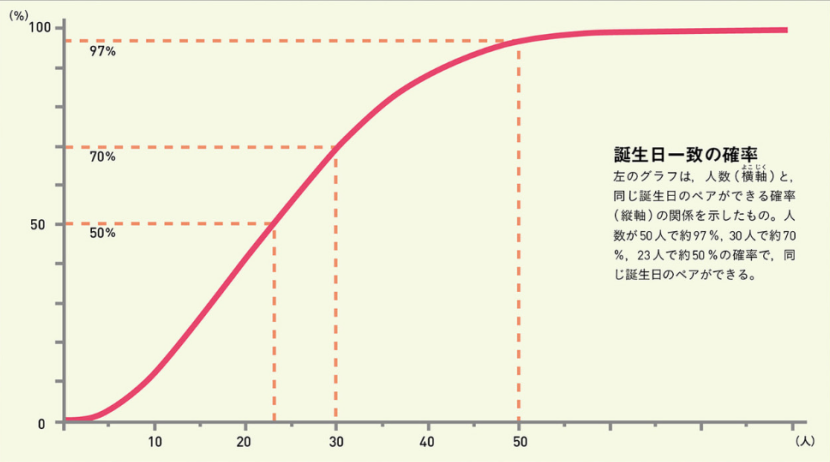
社長は、高価なのものなので1つしか用意できない。1年は365日もある。社員は50人だ。そんな確率はうんと低いんじゃないか?
はい。みなさんはどれくらいの確率だと思いますか?
ベイズ理論
論理的な説明を数字で表現する場合にトーマス・ベイズが生み出したベイズ理論が用いられます。
ベイズ理論は、確率論の一部であり「何かが起こる可能性は、その事柄の過去の発生頻度を使ってほぼ推測ができる」ことだそうです。
先の例もこの数式で算出することができるそうです。
$$ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} $$
ベイズ統計
例えば、ある男性ががんであれば80%の確率で陽性になる検査を受けて陽性の結果が出た場合、その原因が本当にがんである確率を求めることができるそうです。
陽性であっても本当にがんである確率は約4.6%であることがわかるそうです。
計算式が気になる方は本書を手にとって見てください。
おわり
プログラミングの条件式が命題ってことがわかりました。論理的に説明できないと仕様としてコードが書けないってのもありますし、思わぬバグが起きたりも。
パラドックスについては実際に仕様を決めてもあれ…?ここは…と複雑な仕組みになればなるほど矛盾が出そうですね。単に仕様漏れ。という説もありますが。
僕個人としては、論理的思考を養いたい=プログラミングを学びたい人が増えれば嬉しい限りです。
ベイズ統計は、改めてちゃんと理解して色々応用したいと思います。
※文中に書いたコードはGPTに生成してもらいました。